Why Nobody Should Use Sample Covariance Matrices

Table of Contents

Since Harry Markowitz introduced mean-variance optimization in 1952, portfolio managers have faced a persistent and frustrating problem. The mathematical elegance of Modern Portfolio Theory promises optimal asset allocation, but in practice, portfolios constructed using traditional methods often perform worse than simple equal-weight strategies. The culprit? A seemingly innocuous component that lies at the heart of every optimization: the sample covariance matrix.

In their groundbreaking 2003 paper “Honey, I Shrunk the Sample Covariance Matrix,” Olivier Ledoit and Michael Wolf delivered a provocative message that would reshape quantitative portfolio management: nobody should be using the sample covariance matrix for portfolio optimization. This wasn’t hyperbole – it was a mathematically rigorous solution to one of finance’s most persistent practical problems.

The Ledoit-Wolf approach represents more than just a technical improvement; it embodies a fundamental shift in how we think about estimation error and its impact on portfolio construction. By introducing shrinkage techniques borrowed from statistical decision theory, they provided a simple yet powerful method that consistently outperforms traditional approaches while remaining accessible to practitioners.

The Sample Covariance Matrix Problem

The Error Maximization Phenomenon

Traditional portfolio optimization relies on the sample covariance matrix computed from historical returns. While this approach is mathematically straightforward and statistically unbiased, it creates a devastating practical problem that Richard Michaud aptly termed “error maximization.”

The fundamental issue arises when the number of assets is large relative to the number of historical observations – a common situation in modern portfolio management. Under these conditions, the sample covariance matrix becomes unreliable in precisely the way that hurts optimization most. The most extreme coefficients in the matrix tend to take on extreme values not because they reflect true relationships, but because they contain the most estimation error.

Mean-variance optimizers, by their very nature, latch onto these extreme coefficients and place the biggest bets on the most unreliable estimates. This creates a perverse situation where the optimization process systematically amplifies estimation errors, leading to portfolios that look optimal on paper but perform poorly in practice.

The Curse of Dimensionality

The problem becomes more severe as the investment universe expands. Consider a portfolio manager selecting from 500 stocks using 60 months of return data – a typical scenario in institutional asset management. The sample covariance matrix must estimate 125,250 unique parameters from just 60 observations. This ratio of parameters to observations virtually guarantees that estimation error will dominate true signal.

The mathematical reality is stark: when the number of assets approaches or exceeds the number of time periods, the sample covariance matrix becomes not just unreliable but potentially unstable. Eigenvalues can become negative, correlations can exceed realistic bounds, and the resulting optimization can produce wildly unstable portfolio weights that change dramatically with small changes in the data.

The Cost of Estimation Error

Empirical evidence consistently shows that portfolios optimized using sample covariance matrices exhibit several problematic characteristics. They tend to have high turnover as weights fluctuate with estimation noise. They often concentrate in assets with artificially low estimated volatilities or correlations. Most importantly, they frequently underperform simpler strategies that don’t rely on precise covariance estimates.

This performance gap represents more than academic curiosity – it translates directly into reduced returns for investors and undermines confidence in quantitative portfolio management techniques. The promise of mean-variance optimization remains compelling, but traditional implementation methods fail to deliver on that promise.

The Shrinkage Solution

The Conceptual Breakthrough

Ledoit and Wolf’s innovation lies in recognizing that the solution requires balancing two competing objectives: incorporating the rich information in historical data while avoiding the pitfalls of estimation error. Their approach combines the sample covariance matrix with a highly structured alternative through a technique called shrinkage.

The shrinkage estimator takes the form:

$$\hat{\Sigma}_{shrink} = \delta^* F + (1 - \delta^*) S$$

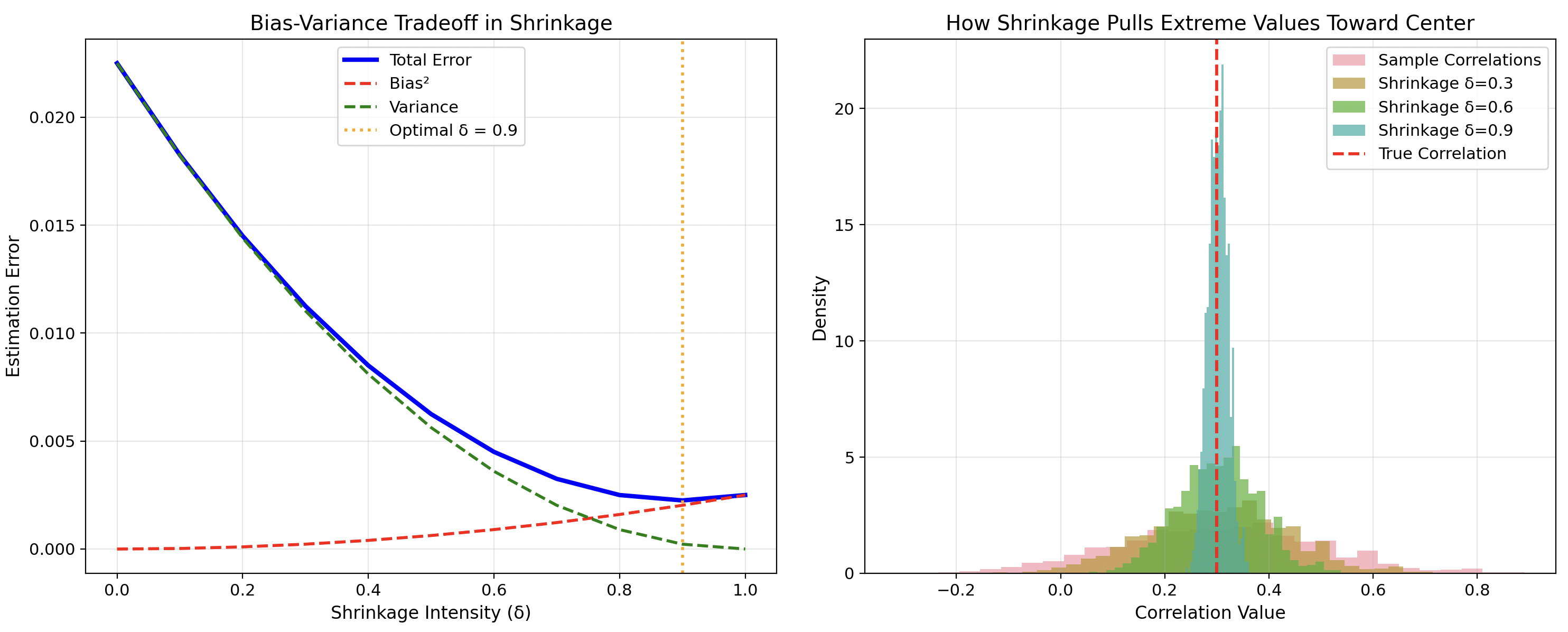
Where $S$ represents the sample covariance matrix, $F$ represents a structured target matrix, and $\delta^*$ represents the optimal shrinkage intensity. This simple linear combination creates a compromise estimator that systematically pulls extreme values toward more reasonable central values.

The beauty of this approach lies in its intuitive appeal and mathematical rigor. By “shrinking” extreme estimates toward a structured center, the method reduces estimation error where it matters most while preserving genuine signal in the data. The challenge lies in determining the optimal shrinkage intensity and choosing an appropriate target.

The Constant Correlation Target

Ledoit and Wolf propose using a constant correlation model as the shrinkage target. This model assumes that all pairwise correlations are identical, estimated as the average of all sample correlations. Combined with individual sample variances, this creates a structured covariance matrix that captures the most important features of asset relationships while using minimal parameters.

The constant correlation model represents an elegant compromise between complexity and parsimony. It acknowledges that assets within a universe often share common factors that create positive correlations, while avoiding the complexity of specifying detailed factor structures. The model requires estimating only one correlation parameter plus individual variances, dramatically reducing the parameter-to-observation ratio.

Optimal Shrinkage Intensity

The most sophisticated aspect of the Ledoit-Wolf approach involves determining the optimal shrinkage intensity $\delta^*$. Rather than arbitrarily choosing a value between 0 and 1, they derive a formula that minimizes the expected distance between the shrinkage estimator and the true (unknown) covariance matrix.

This optimization problem leads to a complex but implementable formula that considers three key components:

• π (pi): The sum of asymptotic variances of sample covariance entries
• ρ (rho): The sum of asymptotic covariances between target and sample entries
• γ (gamma): The misspecification of the shrinkage target

The optimal shrinkage intensity becomes $\delta^* = \frac{\pi - \rho}{\gamma}$, providing a data-driven approach to determining the appropriate balance between sample information and structured estimation.

Theory Validated in Practice

Experimental Design

Ledoit and Wolf conducted comprehensive empirical tests using U.S. stock market data from 1983 to 2002. They constructed value-weighted benchmarks of varying sizes (30, 50, 100, 225, and 500 stocks) and simulated active portfolio management with realistic constraints including long-only positions and position size limits.

To mimic skilled active management, they generated return forecasts by adding controlled noise to realized returns, calibrated to produce an unconstrained information ratio of approximately 1.5. This approach creates a realistic testing environment where the quality of the covariance matrix estimator directly impacts portfolio performance.

Compelling Results

The empirical results provide overwhelming support for the shrinkage approach across all tested scenarios:

Information Ratio Improvements: The shrinkage estimator consistently delivered the highest information ratios across all benchmark sizes. For 30-stock portfolios, the improvement was from 0.97 to 1.24 – a 28% increase. For larger universes, the improvements were even more dramatic, with 500-stock portfolios seeing increases from 0.20 to 0.30.

Risk Reduction: In every scenario, the shrinkage estimator produced the lowest standard deviation of excess returns. This risk reduction occurred without sacrificing expected returns, creating genuine improvements in risk-adjusted performance.

Turnover Benefits: Portfolios constructed using shrinkage exhibited lower turnover than those using sample covariance matrices. This reduction in trading activity translates directly into lower transaction costs and improved net performance.

Statistical Significance

The consistency of results across different market conditions, time periods, and portfolio sizes provides strong evidence for the robustness of the shrinkage approach. The improvements aren’t marginal or dependent on specific market environments – they represent systematic enhancements to the portfolio optimization process.

Importantly, the benefits increase with portfolio complexity. While the improvements for 30-stock portfolios are meaningful, they become dramatic for 500-stock portfolios where estimation challenges are most severe. This pattern confirms that shrinkage addresses the fundamental curse of dimensionality in portfolio optimization.

From Theory to Trading

Computational Simplicity

One of the most appealing aspects of the Ledoit-Wolf approach is its computational simplicity. Unlike complex factor models or proprietary risk systems, shrinkage requires only basic matrix operations and can be implemented using standard mathematical libraries. The authors provide explicit formulas and even offer downloadable code, removing barriers to adoption.

The algorithm follows a straightforward process:

1. Compute the sample covariance matrix from historical returns
2. Calculate the constant correlation target matrix
3. Estimate the optimal shrinkage intensity using the provided formula
4. Combine the matrices using the linear shrinkage formula
5. Use the resulting matrix in standard portfolio optimization

Integration with Existing Systems

The shrinkage estimator integrates seamlessly with existing portfolio optimization frameworks. Managers using quadratic programming software need only replace their covariance matrix input – no changes to optimization procedures, constraint handling, or risk management systems are required.

This compatibility represents a significant practical advantage over alternative approaches like factor models or proprietary risk systems. Organizations can implement shrinkage techniques without expensive system overhauls or lengthy integration projects.

Parameter Sensitivity

Empirical testing reveals that the shrinkage approach is relatively insensitive to parameter choices. The optimal shrinkage intensity formula provides robust results across different market conditions and time periods. Even suboptimal shrinkage intensities typically outperform the sample covariance matrix, providing a margin of safety for practical implementation.

Why Shrinkage Works

Statistical Decision Theory

The shrinkage principle draws from deep results in statistical decision theory, particularly the work of Charles Stein in the 1950s. Stein’s paradox demonstrated that in high-dimensional estimation problems, biased estimators can systematically outperform unbiased alternatives – a counterintuitive result that revolutionized statistical thinking.

Applied to covariance estimation, this insight suggests that the unbiased sample covariance matrix is actually suboptimal in realistic portfolio settings. By introducing bias toward a structured target, shrinkage estimators reduce overall estimation error despite being technically biased.

The Bias-Variance Tradeoff

The success of shrinkage techniques reflects the fundamental bias-variance tradeoff in statistical estimation. The sample covariance matrix is unbiased but has high variance, particularly for extreme coefficients. The constant correlation target is biased but has low variance.

Shrinkage optimally combines these estimators to minimize total estimation error. In mathematical terms, while shrinkage increases bias, it reduces variance by a larger amount, creating a net improvement in estimation accuracy. This tradeoff becomes more favorable as dimensionality increases, explaining why shrinkage benefits are largest for complex portfolios.

Ensemble Effect

The shrinkage approach creates an ensemble effect by averaging multiple correlation estimates. Rather than relying on individual pairwise correlations (which may be poorly estimated), the constant correlation target uses information from all correlations to estimate each relationship. This pooling of information reduces the impact of estimation noise in any single correlation coefficient.

Extensions and Variations

Alternative Shrinkage Targets

While the constant correlation model provides an effective shrinkage target, researchers have explored alternatives including single-factor models, multi-factor structures, and identity matrices. Each target embodies different assumptions about the underlying correlation structure and may be more appropriate for specific asset classes or market conditions.

The choice of shrinkage target involves balancing structure and flexibility. More complex targets can capture additional features of asset relationships but require estimating more parameters, potentially reintroducing estimation error. The constant correlation model strikes an effective balance for most equity portfolio applications.

Dynamic Shrinkage

Recent research has explored time-varying shrinkage intensities that adapt to changing market conditions. During crisis periods when correlations tend to increase, higher shrinkage intensities may be appropriate. During normal periods, lower intensities preserve more information from sample estimates.

Dynamic approaches add complexity but may provide additional performance benefits, particularly during regime changes when historical relationships break down temporarily.

Cross-Asset Applications

The shrinkage principle extends naturally to multi-asset portfolios including bonds, commodities, and alternative investments. However, the constant correlation assumption may be less appropriate when assets come from fundamentally different classes with distinct risk characteristics.

For cross-asset applications, researchers have developed more sophisticated shrinkage targets that account for block structures, where assets within classes are highly correlated but correlations across classes are lower.

Limitations and Considerations

Model Assumptions

The Ledoit-Wolf approach assumes that returns are independently and identically distributed over time with finite fourth moments. While these assumptions are reasonable for many applications, they may be violated during periods of extreme market stress or for assets with complex return dynamics.

Time-varying volatilities, fat tails, and regime changes can affect the performance of shrinkage estimators, though empirical evidence suggests they remain more robust than sample covariance matrices under these conditions.

Parameter Uncertainty

While the optimal shrinkage intensity formula provides data-driven estimates, it still involves uncertainty. The asymptotic nature of the optimality results means performance may vary in finite samples, particularly for very small datasets or unusual market conditions.

Practitioners should view shrinkage as a systematic improvement over traditional methods rather than a perfect solution to covariance estimation challenges.

Computational Considerations

For very large portfolios (thousands of assets), computing the optimal shrinkage intensity can become computationally intensive due to the complex formulas involved. However, simplified approaches using fixed shrinkage intensities often provide most of the benefits with reduced computational requirements.

Impact on Portfolio Management Practice

Industry Adoption

The Ledoit-Wolf shrinkage estimator has been widely adopted across the investment management industry. Major asset managers, pension funds, and institutional investors have incorporated shrinkage techniques into their portfolio construction processes, often reporting significant improvements in risk-adjusted performance.

The approach has been particularly popular in quantitative equity management, where large universes and frequent rebalancing make covariance estimation challenges most acute. However, applications have expanded to include fixed income, multi-asset, and alternative investment strategies.

Academic Influence

The paper has generated extensive academic research exploring variations, extensions, and theoretical refinements of shrinkage techniques. It has become one of the most cited papers in portfolio optimization, influencing both theoretical development and practical implementation of quantitative investment strategies.

Regulatory and Risk Management

The improved stability and robustness of shrinkage-based portfolios have made them attractive for risk management applications. Regulatory frameworks increasingly emphasize robust risk measurement, and shrinkage techniques provide more reliable estimates for value-at-risk and stress testing applications.

Future Directions and Research

Machine Learning Integration

Recent research has explored combining shrinkage techniques with machine learning methods for covariance estimation. Neural networks, random forests, and other algorithms can potentially capture nonlinear relationships and time-varying structures while benefiting from shrinkage regularization.

These hybrid approaches aim to combine the robustness of shrinkage with the flexibility of modern machine learning, though they add significant complexity to implementation and interpretation.

High-Frequency Applications

The principles underlying shrinkage estimation apply naturally to high-frequency trading and intraday portfolio management. However, the specific characteristics of high-frequency data – including microstructure noise, asynchronous trading, and extreme dimensionality – require specialized adaptations of shrinkage techniques.

ESG and Factor Integration

As environmental, social, and governance (ESG) considerations become more important in portfolio management, researchers are exploring how to incorporate these factors into shrinkage-based covariance estimation. The challenge lies in balancing traditional risk factors with ESG constraints while maintaining the robustness benefits of shrinkage.

Conclusion: The Fix That Works

The Ledoit-Wolf shrinkage estimator represents more than just a technical improvement in covariance matrix estimation – it embodies a fundamental shift in how we approach the bias-variance tradeoff in quantitative finance. By demonstrating that systematic bias can improve estimation accuracy in high-dimensional settings, their work challenged conventional wisdom and provided practitioners with a powerful tool for enhanced portfolio performance.

The elegance of the shrinkage approach lies in its simplicity and robustness. Unlike complex factor models or proprietary systems, shrinkage requires minimal assumptions, integrates easily with existing frameworks, and consistently delivers improvements across diverse market conditions and portfolio sizes. The technique democratizes sophisticated risk modeling by making advanced statistical methods accessible to any organization with basic quantitative capabilities.

Perhaps most importantly, the shrinkage estimator restores faith in the fundamental promise of mean-variance optimization. By addressing the estimation error problems that plagued traditional implementations, it allows the theoretical elegance of Modern Portfolio Theory to translate into practical performance improvements. Portfolio managers can once again rely on optimization techniques to deliver the risk-adjusted returns that theory promises.

The broader implications extend beyond portfolio management to any application involving high-dimensional statistical estimation. The principles underlying shrinkage estimation apply to risk modeling, factor analysis, and machine learning applications throughout finance and beyond. Understanding these principles provides valuable insights into the fundamental challenges and opportunities in quantitative analysis.

As markets become more complex and investment universes continue to expand, the importance of robust estimation techniques will only grow. The Ledoit-Wolf contribution provides a foundation for addressing these challenges while maintaining the mathematical rigor and practical applicability that quantitative finance demands. Their work reminds us that sometimes the most powerful innovations come not from adding complexity, but from intelligently managing the complexity that already exists.

For practitioners, the message is clear: the sample covariance matrix should indeed be relegated to history, replaced by shrinkage techniques that systematically improve portfolio performance. The only question is not whether to implement shrinkage, but how quickly organizations can adapt their processes to capture these benefits. In a field where small improvements in risk-adjusted returns translate into substantial economic value, the Ledoit-Wolf contribution represents one of the most significant practical advances in modern portfolio theory.