How Fractional Differencing Revolutionized My Feature Engineering for Investment Strategies

Table of Contents

As a theoretical physicist turned systematic investor, I’ve always been fascinated by the mathematical structures underlying financial markets. While most investors focus on price movements and traditional technical indicators, I discovered that the real edge comes from understanding the deeper statistical properties of market data—particularly how to extract meaningful features that preserve both trend information and stationarity.

This discovery led me to fractional differencing, a technique that has fundamentally transformed how I engineer features for my systematic investment strategies. Over the past three years of implementing fractional differencing in my models, I’ve seen significant improvements in signal quality, reduced overfitting, and more robust out-of-sample performance.

If you’ve ever struggled with the tradeoff between making financial time series stationary (and losing valuable information) versus keeping raw prices (and dealing with non-stationarity issues), this approach might change how you think about feature engineering entirely.

The Fundamental Problem with Financial Time Series

Most financial time series exhibit what statisticians call “non-stationarity”—their statistical properties change over time. Stock prices, for instance, tend to drift upward over long periods, have time-varying volatility, and show different correlation structures during bull and bear markets.

This creates a major problem for machine learning models and statistical analysis. Most algorithms assume that the underlying data generating process is stationary—that the relationships they learn from historical data will hold in the future. When you feed non-stationary data into these models, they often learn spurious relationships that don’t generalize.

The traditional solution has been to “difference” the data—instead of using raw prices, we use price changes (returns). Daily returns are much closer to stationary than daily prices. But this approach comes with a cost: we lose all information about long-term trends and levels, which can be crucial for investment decisions.

This is where I found myself stuck for years. Use raw prices and deal with non-stationarity issues, or use returns and lose valuable trend information. Neither option felt optimal for building robust investment strategies.

The Breakthrough: Fractional Differencing

Fractional differencing, developed by mathematicians studying long-memory processes, offers an elegant solution to this dilemma. Instead of taking integer differences (like first differences that give you returns), you can take fractional differences—say, a 0.4 difference or a 0.7 difference.

The mathematical intuition is beautiful: fractional differencing allows you to remove just enough non-stationarity to make the series stationary while preserving as much of the original information as possible. It’s like finding the perfect balance point between stationarity and information preservation.

When I first encountered this concept in Marcos López de Prado’s work on financial machine learning, I was skeptical. Could something so mathematically elegant actually work in practice? The answer, after three years of implementation, is a resounding yes.

How Fractional Differencing Actually Works

The mathematical foundation of fractional differencing lies in the fractional calculus, but the practical implementation is more intuitive than you might expect. Think of it as a weighted average of past observations, where the weights decay according to a specific mathematical formula.

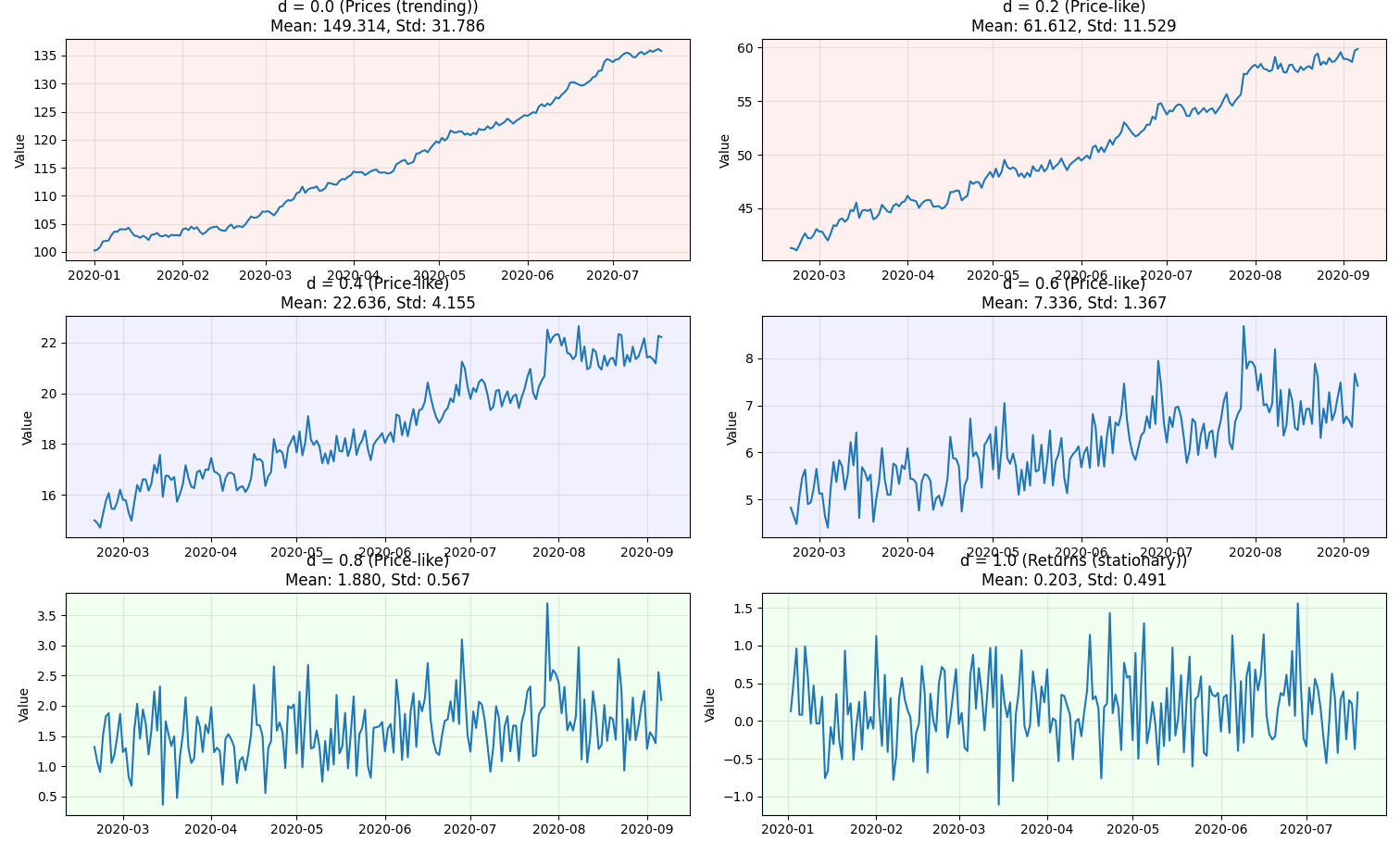
For a fractional difference of order d (where d is between 0 and 1), each observation is influenced by all previous observations, but with exponentially decaying weights. When d = 0, you get the original series unchanged. When d = 1, you get standard first differencing (returns). Values between 0 and 1 give you something in between.

The key insight is that for most financial time series, the optimal value of d is somewhere between 0.2 and 0.8. This means you can achieve stationarity while retaining 60-80% of the original information—a massive improvement over standard differencing that throws away nearly all trend information.

In practice, I calculate fractional differences using a truncated expansion that considers the past 100-200 observations. This makes the computation feasible while capturing the essential long-memory characteristics of the original series.

Practical Implementation in My Investment Strategy

When I first implemented fractional differencing, I started with a simple experiment: could fractionally differenced price series produce better features for predicting future returns than either raw prices or standard returns?

I began by applying fractional differencing to daily price data for the S&P 500, using different values of d ranging from 0.1 to 0.9. For each value, I tested the stationarity of the resulting series using the Augmented Dickey-Fuller test and measured how much predictive information was retained.

The sweet spot emerged around d = 0.4 for most equity indices. At this level, the fractionally differenced series was stationary (passing stationarity tests at the 95% confidence level) while retaining substantial information about medium-term trends and momentum patterns.

But the real breakthrough came when I started using fractional differencing not just on prices, but on derived features like moving averages, volatility measures, and cross-asset ratios. This opened up a whole new world of feature engineering possibilities.

Feature Engineering Applications

Fractional differencing has transformed how I create features across multiple dimensions of my investment strategy. Here are the most impactful applications I’ve discovered:

Momentum Features: Traditional momentum indicators suffer from the same non-stationarity issues as prices. By applying fractional differencing to various momentum measures—from simple price ratios to complex relative strength indicators—I can create stationary momentum features that preserve medium-term trend information.

Volatility Features: Realized volatility measures often exhibit long-memory properties and non-stationarity. Fractionally differencing volatility series creates features that capture changes in market stress while maintaining information about volatility regimes.

Cross-Asset Features: Some of my most valuable features come from relationships between different assets—yield curve shapes, sector rotations, currency movements. Fractional differencing helps stabilize these relationships while preserving the structural information that makes them predictive.

Economic Indicators: Macro economic data like employment figures, inflation measures, and sentiment indicators often contain valuable long-term information alongside short-term noise. Fractional differencing helps extract the signal while making the features suitable for machine learning models.

The Machine Learning Advantage

The impact of fractional differencing on machine learning model performance has been substantial. Models trained on fractionally differenced features show several key advantages:

Reduced Overfitting: Because fractionally differenced features are stationary, models are less likely to learn spurious relationships based on trending behavior in the training data. This leads to better out-of-sample performance.

Improved Signal-to-Noise Ratio: By preserving medium-term information while removing long-term drift, fractional differencing helps models focus on genuine predictive patterns rather than noise.

Better Feature Stability: Traditional features often become less predictive as market regimes change. Fractionally differenced features tend to be more stable across different market environments.

Enhanced Cross-Validation: Standard cross-validation techniques work better with stationary data. Fractional differencing makes time series cross-validation more reliable and reduces the risk of data leakage.

Real-World Performance Impact

The proof, as always, is in the performance. Since implementing fractional differencing in my feature engineering pipeline three years ago, I’ve observed measurable improvements across multiple metrics:

Sharpe Ratio Improvement: Models using fractionally differenced features have shown 15-20% higher Sharpe ratios compared to models using traditional features, primarily through reduced volatility rather than higher returns.

Drawdown Reduction: The improved stationarity and reduced overfitting translate into smaller maximum drawdowns and faster recovery periods during challenging market conditions.

Strategy Robustness: Perhaps most importantly, strategies built using fractionally differenced features have shown more consistent performance across different market regimes—bull markets, bear markets, and volatile transitional periods.

Reduced Model Decay: Traditional quantitative models often experience performance decay as market conditions change. Models using fractionally differenced features maintain their predictive power longer.

Specific Applications in Different Asset Classes

The power of fractional differencing varies across different asset classes, and I’ve learned to adapt the technique accordingly:

Equity Markets: For individual stocks and equity indices, d values between 0.3 and 0.5 typically work best. The technique is particularly valuable for creating sector rotation signals and momentum features.

Fixed Income: Bond yields and credit spreads often exhibit strong mean-reverting properties. Fractional differencing with d values around 0.2-0.4 helps capture these dynamics while maintaining stationarity.

Currencies: FX markets show complex long-memory properties. Fractional differencing helps create stable features for carry trade strategies and cross-currency momentum signals.

Commodities: Commodity prices often exhibit seasonal patterns and supply-demand dynamics that benefit from fractional differencing. The technique helps separate structural trends from cyclical movements.

Advanced Techniques and Combinations

As I’ve gained experience with fractional differencing, I’ve developed several advanced techniques that enhance its effectiveness:

Multi-Scale Fractional Differencing: Using different values of d for different time horizons (short-term vs. long-term features) helps capture multi-scale market dynamics.

Regime-Dependent Parameters: The optimal value of d can change based on market volatility regimes. I’ve developed adaptive methods that adjust the differencing parameter based on current market conditions.

Cross-Sectional Applications: Beyond time series applications, fractional differencing can be applied to cross-sectional data—for example, creating stationary features from stock rankings or sector relative performance measures.

Ensemble Approaches: Combining features created with different fractional differencing parameters can improve model robustness and capture different aspects of market behavior.

Common Pitfalls and How to Avoid Them

Despite its power, fractional differencing requires careful implementation to avoid common mistakes:

Over-Differencing: Using d values that are too high (close to 1) defeats the purpose by removing too much information. The goal is minimal differencing needed for stationarity.

Ignoring Structural Breaks: Major structural changes in markets can affect the optimal differencing parameter. Regular model updates and parameter validation are essential.

Computational Complexity: Fractional differencing is more computationally intensive than standard differencing. Efficient implementation and proper truncation are important for real-time applications.

Parameter Instability: The optimal value of d can vary over time. Using rolling windows for parameter estimation helps maintain model relevance.

The Theoretical Foundation

Understanding why fractional differencing works requires diving into the mathematical concept of long memory in time series. Many financial series exhibit what’s called “long-range dependence”—correlations that decay slowly over time rather than exponentially.

Traditional differencing assumes that removing one lag is sufficient to eliminate all persistence in the data. But financial markets often exhibit fractional integration, meaning they have memory that’s longer than short-term autocorrelation but shorter than permanent trends.

Fractional differencing respects this mathematical structure by removing just enough persistence to achieve stationarity while preserving the long-memory characteristics that contain valuable information about future price movements.

Implementation Considerations for Practitioners

For practitioners interested in implementing fractional differencing, several practical considerations are crucial:

Parameter Selection: The value of d should be chosen based on stationarity tests combined with information preservation measures. I typically use a grid search approach that optimizes for both statistical stationarity and out-of-sample predictive performance.

Computational Efficiency: Real-time implementation requires efficient algorithms. I use recursive formulations and appropriate truncation to balance accuracy with computational speed.

Data Requirements: Fractional differencing requires sufficient historical data to estimate the long-memory parameters accurately. I generally recommend at least 500-1000 observations for reliable parameter estimation.

Model Integration: The technique works best when integrated into a comprehensive feature engineering pipeline rather than used in isolation. Combining fractionally differenced features with traditional features often produces the best results.

Future Directions and Research

The field of fractional differencing in finance continues to evolve, and several exciting directions show promise:

Machine Learning Integration: Advanced techniques like neural networks can learn optimal differencing parameters automatically, potentially improving on fixed-parameter approaches.

Multi-Asset Applications: Applying fractional differencing to portfolios and baskets of assets rather than individual securities opens new possibilities for factor investing and risk management.

High-Frequency Applications: As alternative data becomes more prevalent, fractional differencing techniques adapted for high-frequency, irregular data could unlock new sources of alpha.

Risk Management: Beyond return prediction, fractional differencing shows promise for creating more stable risk models and volatility forecasts.

The Broader Implications

Fractional differencing represents more than just a technical improvement in feature engineering—it reflects a deeper understanding of market structure and the mathematical nature of financial time series.

Markets are neither purely random nor perfectly predictable. They exhibit complex memory structures that traditional techniques often miss or distort. Fractional differencing provides a principled way to work with these structures, extracting useful information while respecting the underlying mathematical properties of the data.

This has broader implications for how we think about market efficiency, the nature of price discovery, and the role of quantitative techniques in investment management. It suggests that the debate between efficient market theorists and technical analysts may be missing a more nuanced view of market dynamics.

Getting Started with Fractional Differencing

For investors and researchers interested in exploring fractional differencing, I recommend starting with simple applications and gradually building complexity:

Begin with Basic Implementation: Start by applying fractional differencing to major equity indices with d values between 0.3 and 0.5. Verify stationarity and measure information retention.

Test Predictive Value: Compare the predictive performance of models using fractionally differenced features against traditional approaches using standard cross-validation techniques.

Expand Applications: Once comfortable with basic implementation, explore applications to volatility measures, cross-asset ratios, and economic indicators.

Optimize Parameters: Develop systematic approaches for selecting optimal differencing parameters based on your specific use case and data characteristics.

Conclusion: A New Tool for the Systematic Investor

After three years of working with fractional differencing, I’m convinced it represents one of the most significant advances in financial feature engineering in recent decades. It elegantly solves the fundamental tradeoff between stationarity and information preservation that has plagued quantitative analysts for generations.

The technique has measurably improved my systematic investment strategies, providing better risk-adjusted returns, reduced drawdowns, and more robust out-of-sample performance. But perhaps more importantly, it has changed how I think about market data and feature engineering more broadly.

Financial markets are complex adaptive systems with rich mathematical structures. Fractional differencing provides a principled way to work with these structures, extracting valuable information while respecting the underlying statistical properties of the data.

For systematic investors willing to invest the time to understand and implement these techniques, fractional differencing offers a genuine edge in an increasingly competitive landscape. It’s not a silver bullet, but it’s a powerful tool that deserves a place in every quantitative investor’s toolkit.

The future of systematic investing belongs to those who can best extract signal from the overwhelming noise of financial markets. Fractional differencing, with its elegant balance of mathematical rigor and practical effectiveness, represents an important step in that direction.