Carry Strategies Across Asset Classes: Mathematical Foundations

Table of Contents

Imagine borrowing money at 1% and lending it at 5%. The 4% difference seems like an obvious profit, yet financial theory suggests this opportunity shouldn’t exist. Markets should quickly eliminate such discrepancies through arbitrage. But across currencies, bonds, and stocks, these “carry” opportunities persist with remarkable consistency.

Carry strategies represent one of the most fundamental patterns in financial markets. Whether we examine Japanese yen funding trades, Treasury yield curve strategies, or high-dividend stock portfolios, the same underlying principle drives returns: systematic violations of theoretical pricing relationships that persist because they reflect genuine risk compensation.

This persistence across asset classes and decades suggests something deeper than temporary market inefficiency. Instead, carry strategies tap into a fundamental feature of how markets price risk and uncertainty, creating opportunities for disciplined investors who understand both the rewards and the dangers.

Part I: The Universal DNA of Carry

The Core Principle

Every carry strategy, regardless of asset class, exploits the same basic mathematical relationship. In theory, when you earn a higher yield on an investment, that extra income should be exactly offset by capital losses. The beauty of carry strategies is that this offsetting rarely happens completely.

Consider any investment that pays a higher yield than the risk-free rate. Efficient market theory predicts that higher yields will be offset by price declines, leaving risk-adjusted returns equal across all investments. In mathematical terms:

$$\text{Total Return} = \text{Yield Income} + \text{Price Change}$$

Theory requires these components to offset each other perfectly, but empirical reality shows they don’t. Yield income consistently exceeds the magnitude of offsetting price changes, creating the mathematical foundation for carry strategies.

Why the Theory Fails

The failure of perfect offsetting occurs because carry strategies systematically bear specific types of risk. These risks share common characteristics across all asset classes: they tend to materialize during crisis periods, exhibit sudden and large losses, and correlate with broader market stress.

This creates what mathematicians call a “risk premium” - extra compensation for bearing unpleasant risks that most investors prefer to avoid. The risk premium explains why carry opportunities persist despite being well-known and widely studied.

The Universal Pattern

Across currencies, bonds, and stocks, carry strategies exhibit similar return characteristics. They generate steady positive returns most of the time, punctuated by occasional large losses during market stress. This creates negatively skewed return distributions where the average outcome is positive, but tail risks are substantial.

Understanding this pattern is crucial for successful implementation. Carry strategies aren’t free money - they’re compensation for bearing specific risks that can be managed but never eliminated.

Part II: Currency Carry - The Foundation Case

The Interest Rate Puzzle

Currency carry trades exploit one of finance’s most persistent puzzles. According to Uncovered Interest Rate Parity (UIP) theory, currencies with higher interest rates should weaken by exactly the interest rate differential. If Japan offers 1% rates and Australia offers 5%, the Australian dollar should depreciate by 4% annually to eliminate arbitrage opportunities.

The mathematical relationship should be:

$$E_t[s_{t+1} - s_t] = i_t^{domestic} - i_t^{foreign}$$

Where $s_t$ is the exchange rate and $i_t$ represents interest rates. In reality, this relationship fails spectacularly. Empirical evidence shows the opposite pattern:

$$s_{t+1} - s_t = \alpha + \beta(i_t^{foreign} - i_t^{domestic}) + \epsilon_{t+1}$$

Where theory requires $\beta = -1$, but empirical estimates consistently show $\beta > 0$, often around +0.3. This positive coefficient creates the foundation of currency carry strategies - currencies with higher interest rates tend to strengthen rather than weaken.

How Currency Carry Works

A currency carry trade involves borrowing in a low-yielding currency and investing in a high-yielding currency. The total return can be decomposed as:

$$R_{t+1}^{carry} = (i_t^{foreign} - i_t^{domestic}) + (s_{t+1} - s_t)$$

The first term represents the interest rate differential (certain at time t), while the second captures exchange rate movements (uncertain but historically biased in favor of carry trades).

For example, borrowing Japanese yen at 1% to buy Australian dollars earning 5% provides a 4% interest differential. If the Australian dollar remains stable or strengthens, the total return exceeds 4%. Even if the Australian dollar weakens moderately, the trade can remain profitable.

The persistence of this pattern across decades and currency pairs suggests that currency carry trades bear systematic risks that justify the premium returns.

The Crash Risk Reality

Currency carry strategies work most of the time but can experience devastating losses during crisis periods. These crashes typically occur when investors flee to safety, unwinding leveraged positions and causing high-yielding currencies to plummet.

The 2008 financial crisis provided a stark example. Currency carry trades lost over 25% in a matter of months as investors rushed to repay low-yielding funding currencies like the yen and Swiss franc. This crash risk explains why currency carry generates positive returns on average - it compensates investors for bearing the risk of sudden, large losses.

Part III: Bond Carry - Term Structure Arbitrage

The Yield Curve Opportunity

Bond carry strategies exploit the typical upward slope of yield curves. In most economic environments, longer-term bonds offer higher yields than shorter-term bonds, creating an apparent opportunity to borrow short and lend long.

The Expectations Hypothesis suggests this opportunity shouldn’t exist. According to this theory, yield curve slopes reflect pure interest rate expectations. If long-term rates are higher than short-term rates, it’s only because short-term rates are expected to rise, eliminating any advantage from extending duration.

Mathematical evidence overwhelmingly rejects this hypothesis. When yield curves are steep, long-term bonds consistently outperform short-term bonds, creating the foundation for bond carry strategies.

The Mathematics of Bond Carry

Bond carry strategies involve capturing the yield curve’s slope while managing interest rate risk. The expected return from extending duration can be expressed as:

$$E[R_{t+1}^{carry}] = (y_t^{(n)} - y_t^{(1)}) - E[\Delta y_{t+1}^{(n)} \cdot D^{(n)}]$$

Where the first term represents the yield pickup from longer maturities and the second captures potential capital loss from rising yields, adjusted by duration $D^{(n)}$.

The trade becomes profitable when:

$$\frac{y_t^{(n)} - y_t^{(1)}}{D^{(n)}} > E[\Delta y_{t+1}^{(n)}]$$

This condition states that the annualized yield pickup must exceed the expected yield increase. Empirically, this holds consistently because yield curves contain term premiums that compensate investors for interest rate uncertainty.

These risk premiums, known as term premiums, vary over time with economic uncertainty. When term premiums are high, bond carry strategies generate higher expected returns. When term premiums compress, carry strategies face headwinds.

Implementation Considerations

Practical bond carry implementation requires managing duration risk through curve positioning strategies. Rather than simply buying long-term bonds, sophisticated approaches involve constructing duration-neutral portfolios that isolate pure carry returns from parallel yield curve shifts.

These strategies might involve owning intermediate-term bonds while shorting both short-term and long-term bonds, creating positions that profit from yield curve changes while maintaining limited sensitivity to overall interest rate movements.

Part IV: Equity Carry - The Dividend Yield Premium

The Growth Offset Myth

Equity carry strategies challenge the assumption that higher dividend yields are offset by lower growth prospects. According to dividend discount models, stocks with higher yields should exhibit lower growth rates, leaving expected returns unchanged across the dividend yield spectrum.

The Gordon Growth Model expresses this relationship mathematically:

$$\text{Expected Return} = \text{Dividend Yield} + \text{Growth Rate}$$

If markets are efficient, this equation implies that dividend yields shouldn’t predict returns because higher yields would be offset by lower growth.

Extensive empirical evidence contradicts this prediction. Stocks with higher dividend yields consistently outperform those with lower yields, both in cross-sectional comparisons and over time. This outperformance forms the basis for equity carry strategies.

The Cross-Sectional Approach

Equity carry strategies typically involve constructing long-short portfolios based on dividend yields or earnings yields. These strategies buy stocks with high yields and sell stocks with low yields, capturing the systematic return premium associated with yield differences.

The challenge lies in constructing factor-neutral portfolios that isolate yield effects from other systematic factors like size, value, or momentum. This requires sophisticated portfolio construction techniques that match factor exposures while maximizing yield differentials.

Successful equity carry strategies also account for sector and style rotations that can temporarily overwhelm yield effects. During growth-oriented market periods, high-yield stocks may underperform despite their attractive fundamental characteristics.

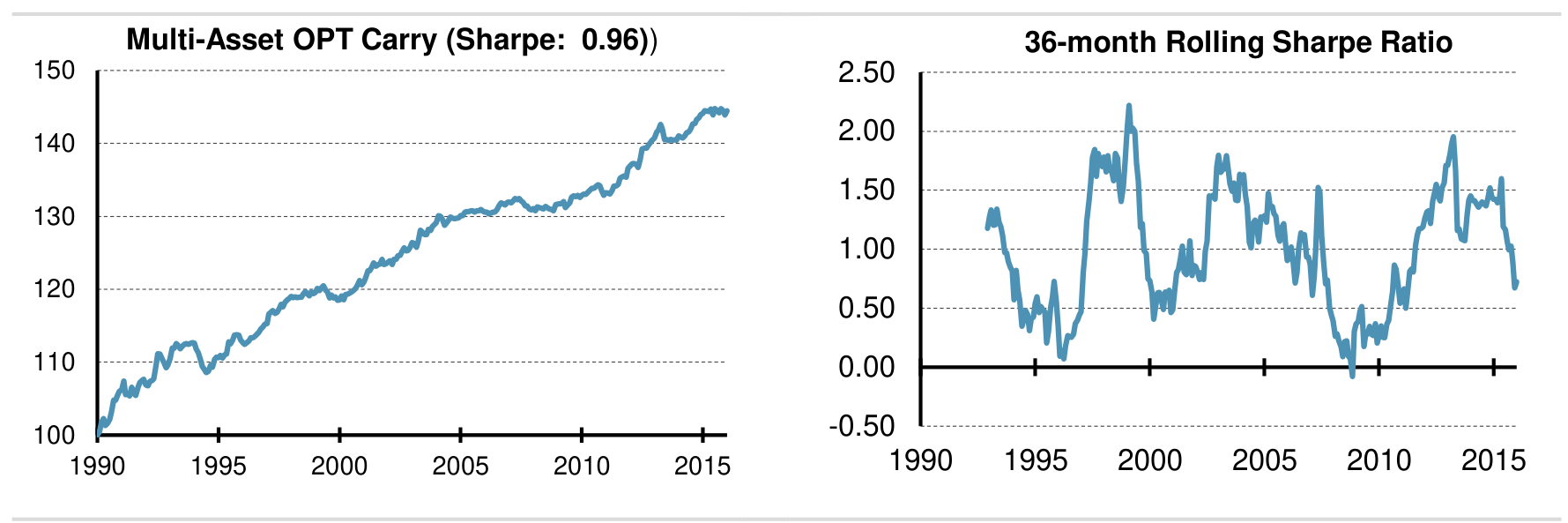
The Risk Premium Explanation

The outperformance of high-yield stocks reflects compensation for bearing specific risks. High dividend yield stocks tend to be mature companies with limited growth opportunities but stable cash flows. These companies systematically face risks related to economic cycles, technological disruption, and changing investor preferences.

During periods when investors favor growth over income, high-yield strategies can experience significant underperformance. This cyclical risk, combined with the fundamental risks of mature businesses, justifies the premium returns that equity carry strategies generate over time.

Part V: Constructing Optimal Carry Portfolios

The Multi-Asset Opportunity

The ultimate sophistication in carry strategies involves combining exposures across asset classes into unified portfolios. This approach recognizes that currency carry, bond carry, and equity carry represent different manifestations of the same underlying risk premium.

Multi-asset carry portfolios can provide superior diversification because the specific risks that drive each carry component don’t always coincide. Currency carry might struggle during emerging market crises while bond carry remains profitable. Equity carry might underperform during growth rallies while currency carry continues generating returns.

Understanding Correlation Dynamics

The key to successful multi-asset carry lies in understanding how correlations between carry strategies change over time. During normal market conditions, correlations remain moderate, providing genuine diversification benefits. During crisis periods, correlations spike dramatically, reducing diversification exactly when it’s needed most.

This time-varying correlation structure is crucial for risk management. Portfolios that appear well-diversified during calm periods can become highly concentrated during stress periods, creating the potential for synchronized losses across all carry components.

Risk Management Framework

Effective carry portfolio management requires sophisticated risk management that accounts for the strategies’ negative skewness and fat tails. Traditional risk measures like standard deviation severely underestimate carry strategies’ true risk because they don’t capture tail risk adequately.

Advanced risk measures provide better estimates:

Value at Risk (VaR): $\text{VaR}_\alpha = -\inf{x : P(R \leq x) \geq \alpha}$

Expected Shortfall (ES): $\text{ES}_\alpha = -E[R | R \leq -\text{VaR} ]$

For carry strategies, Expected Shortfall is particularly important because it captures not just the probability of large losses but their expected magnitude.

Dynamic position sizing can provide crucial protection:

$$w_t = w_{target} \cdot \min\left(1, \frac{\sigma_{target}}{\sigma_{realized}}\right) \cdot \min\left(1, \frac{\text{VIX}_{long-term}}{\text{VIX}_t}\right)$$

This framework automatically reduces leverage when realized volatility or implied volatility exceeds normal levels.

Part VI: The Economics of Carry Risk Premiums

Why Carry Strategies Persist

The mathematical evidence for carry strategies’ profitability is overwhelming, but understanding why they persist requires economic intuition. If these opportunities are so attractive and well-known, why don’t arbitrageurs eliminate them?

The answer lies in the specific characteristics of carry risks. These risks tend to materialize during crisis periods when capital is scarce and risk tolerance is low. They require leverage to generate meaningful returns, creating funding constraints during stress periods. They exhibit negative skewness that challenges many investors’ risk tolerance.

These characteristics create natural limits to arbitrage that prevent carry opportunities from being eliminated. Even sophisticated investors face constraints that limit their ability to fully exploit carry premiums, allowing these opportunities to persist.

The Behavioral Component

Carry strategies also persist due to behavioral factors that influence investor decision-making. The steady profits followed by occasional large losses create a return pattern that many investors find difficult to stomach. Loss aversion and recency bias cause many investors to abandon carry strategies exactly when they’re most attractive.

Professional investors face additional behavioral constraints through career risk and agency problems. Fund managers who experience carry crashes may lose assets or employment, creating incentives to avoid strategies with negative skewness even when they offer positive expected returns.

The Systematic Nature

Perhaps most importantly, carry strategies persist because they’re not pure arbitrage opportunities but systematic exposures to specific risk factors. These risk factors represent fundamental features of how markets price uncertainty and can’t be eliminated through arbitrage.

Currency carry bears crash risk and funding liquidity risk. Bond carry bears interest rate risk and term structure risk. Equity carry bears fundamental risk and style rotation risk. These risks represent genuine economic phenomena that require compensation, ensuring that carry premiums persist over time.

Conclusion: The Enduring Mathematics of Carry

Carry strategies reveal a fundamental truth about financial markets: beneath the complexity of asset pricing lies a simple, elegant pattern. The same basic principle drives returns across all asset classes, yet manifests differently due to each market’s unique characteristics.

The mathematical foundations rest on systematic violations of theoretical pricing relationships that persist because they reflect genuine risk compensation. Understanding these foundations provides crucial insights for both theoretical development and practical implementation.

The universality of carry suggests these strategies tap into fundamental features of how markets price risk and uncertainty. The correlation structure creates both opportunities and risks that must be carefully managed through sophisticated frameworks that go beyond traditional portfolio theory.

For practitioners, carry strategies offer compelling risk-adjusted returns when implemented with proper understanding of their risk characteristics. The key lies not in viewing carry as free money, but as compensation for bearing specific, well-defined risks that can be managed through disciplined approaches.

The future of carry strategies will likely involve increasingly sophisticated techniques for signal enhancement, risk management, and dynamic allocation. Yet the core insight will remain unchanged: markets systematically reward investors who are willing and able to bear the specific risks that carry strategies entail.

Understanding carry strategies thus provides more than just a pathway to attractive returns. It offers insights into the fundamental structure of financial markets and the persistent patterns that govern asset pricing across different markets and time periods. In a world where true arbitrage opportunities are rare, carry strategies represent one of the most robust approaches to generating systematic returns across financial markets.